7 Sugu izplatības (dzīvotņu piemērotības) modeļi
Šajā nodaļā aprakstīta sugu izplatības modelēšanas pieeja no sugai specifiskās modeļos iekļaujamās vides aprakstiem (EGV), caur modeļu parametrizāciju un labākās izvēli, līdz modeļu rezultātu izvērtēšanai nepieciešamās informācijas sagatavošanai.
Iegūtie ik-sugas izplatības modeļi apkopoti, vizualizēti un konspektīvi aprakstīti nodaļas Rezultāti pirmajā apakšnodaļā Individuālu sugu rezultāti. Izplatības modelēšanai izmantotās klātbūtnes vietas, to apkopošanas un filtrēšanas procedūras raksturotas nodaļā Novērojumu atlase, specifiskās - par uzticamām klātbūtnes vietām uzskatāmo atlases soļi ir tās apakšnodaļā Novērojumu atlases gaita, savukārt to dalījums modeļa apmācības un neatkarīgās testēšanas kopā un katras no tām papildināšana ar vidi-kopumā aprakstošām nejaušās izlozes vietās ir apakšnodaļā Modelēšanas datu saglabāšana un procesa vizualizēšana.
Ekoģeogrāfiskie mainīgie, kuru sagatavošanas procedūras un tajos iekļauto vides raksturojumu apraksti ir nodaļā Ekoģeogrāfiskie mainīgie, ir gatavoti mērķtiecīgai sugu izplatības modelēšanai - pirms pašas EGV sagatavošanas ir sastādīts no modelēšanai sākotnēji plānoto sugu (nodaļa Sugu saraksts un pamata apraksti) nepieciešamībām izrietošs plāns. Tas ir apskatāms šajā failā, kurā ir redzams, ka daļa EGV ir veidoti vienkārši plūsmas ērtībai vai domājot arī par citām, ne tikai putnu sugām. Diemžēl pirms EGV ir sagatavoti, nav zināms vai tie visi būs faktiski izmantojami sugu izplatības modelēšanai, tādēļ pirms tās uzsākšanas pārbaudīta ik sugas modeļos iekļaujamo EGV vērtību savstarpējā neatkarība aprēķinot dispersijas ietekmētības faktoru (variance inflation factor; VIF), turpmākam darbam izvēlot tikai pietiekoši neatkarīgos, kuriem veikta indikatīva testēšana to iekļaušanai sugu izpla’tibu prognozējošajos modeļos. Vairāk - šīs nodaļas Sākotnēji izvēlēto pazīmju neatkarība un EGV atlases otrā kārta apakšnodaļā.
Pēc EGV izvēles, veikta sugu izplatības modeļu parametrizācija maximuma entropijas analīzes ietvarā (Phillips et al., 2004). Analīzes gaita, parametrizācijas pieejas un pieņemtie lēmumi ar ieviešanas procedūru (komandu rindām) ir raksturoti šīs nodaļas Modeļa parametrizācija, izvēle un izvērtēšanas apraksti apakšnodaļā. Šīs procedūras ietvaros, izvēlēts modelis, kurš vislabāk spēj raksturot interesējošās sugas izplatību, izšķirot tai piemēroto un nepiemēroto dzīvotņu projekcijas ģeogrāfiskajā telpā (nosedzot visu Latvijas iekšzemes teritoriju 100 m izšķirtspējā).
Part labāko atzītajam modelim sagatavoti dažādi klasifikācijas spējas raksturojumi, raksturojot sagaidāmo kļūdu apjomu gan modeļa apmācībai izmantotajos (un iekšējās validācijas), gan neatkarīgās testēšanas datos. Sniegti ieteikumi izmantojamajiem dzīvotņu piemērotības klasifikācijas sliekšņiem ar izmešanas un pieskaitīšanas kļūdām kā arī kopējo klasifikācijas statistisko nozīmīgumu. Papildus tam, raksturotas projicētās dzīvotņu piemērotības gradienta īpašības un individuālu novērojumu ietekme modelī, kas turklāt vērtētas kontekstā ar nulles modeļiem informācijas telpas nozīmīguma novērtēšanai. Nedaudz plašāk šie mēri un to interpretācija aprakstīti rezultātu nodaļā (Individuālu sugu rezultāti), to izvēles pamatojums un izmantotās analītiskās pieejas (ar komandu rindām) raksturotas šīs nodaļas Nulles modelis.
Šīs nodaļas noslēgumā (Labākā modeļa rezultāti) sniegtas komandu rindas rezultātu nodaļā izmantoto attēlu sagatavošanai.
7.1 Sākotnēji izvēlēto pazīmju neatkarība un EGV atlases otrā kārta
Jebkurā prognostiskā statistiskajā modelī, kuram ir nepieciešama gan ekstrapolācijas, gan skaidrošanas spēja, regresoriem ir jābūt savstarpēji neatkarīgiem (McElreath, 2020), (Zuur et al., 2009). Turklāt, modelī nav pamata atrasties pazīmēm, kuras nepiedalās sugas izplatības prognozēšanā vai sniedz niecīgu pienesumu - jo vairāk EGV, jo skaitļošanā izaicinošāks un resursu ietilpīgāks ir jebkurš izstrādājamais modelis.
Pazīmju neatkarības izvērtējums sniegts nodaļā Multikolinearitāte, savukārt modelī iekļaujamo pazīmju izvēle - EGV indikatīvā nozīme kompleksā modelī.
7.1.1 Multikolinearitāte
Lai gan nereti statistiskajos modeļos par neatkarīgām tiek pieņemtas pazīmes, kuru dispresijas efektīvi neprognozē jebkāda kopa ar citām pazīmēm, to raksturojot ar \(\text{VIF} \le 4\) (Zuur et al., 2009), vides ekoģeogrāfiskajiem mainīgajiem, to telpiskā novietojuma īpašību dēļ, tik zemas vērtības ievērojami ierobežo pieejamo pazīmju loku (Wikle et al., 2019). Maksimuma entropijas analīze tiek uzskatīta par relatīvi robustu pret EGV savstarpējām korelācijām (Phillips et al., 2004), (Phillips et al., 2006), tomēr, lai novērstu spēcīgi ietekmētus modeļa parametru vērtējumus (Montgomery et al., 2012), izvēlējos tikai tos sākotnēji ieplānotos EGV, kuru \(\text{VIF} \le 10\), sekojot (Avotins et al., 2022), (Avotiņš, 2019a) un (Bergmanis et al., 2021) piemēriem.
Šī izvēle veikta R pakotnē {usdm} (Naimi et al., 2014), izmantojot sekojošajā koda apgabalā sniegtās komandu rindas. Darba gaitā no kopējās EGV izvēles tabulas, sagatavota katrai sugai individuāla, tajā pierakstot turpmākam darbam izvēlēto EGV aprēķinātās VIF vērtības. To aprēķināšanai izmantota soli-pa-solim EGV izslēgšanas pieeja sākot ar EGV ar lielāko VIF vērtību un turpināta līdz visām atlikušajām pazīmēm, nejauši izlozētos 20 000 punktos, aprēķināta \(\text{VIF} \le 10\). Pēc noklusējuma programmatūra paredz 5000 nejauši izlozētu punktu izmantošanu, kas palielināts, lai uzlabotu vides aptveri un iegūtā rezultāta stabilitāti neatkarīgos atkārotjumos. Tam, protams, ir cena - skaitļošanai nepieciešamie resursi un laiks ir lielāks.
Šī ir uzskatāma par semi-automatizētu pieeju, kurā sākotnējā (sevišķi plašā) EGV izvēle ir veikta specifiski domājot par ik sugas ekoloģiju un tās izplatību potenciāli atšķirīgi ietekmējošiem dažādiem biotopiem (vides heterogenitāti), tomēr specifiski modelēšanā iekļaujamo pazīmju loks ir izvēlēts automatizēti. Tas nozīmē, ka izvēlēto pazīmju loks var nebūt optimāls specifiski sugas ekoloģiskās nišas aprakstīšanai, tomēr nodrošina statistiskās nepieciešamības un atkarībā modeļa spējas aprakstiem var būt piemērots kā izplatības modeļa ievade (Guisan et al., 2017). Turklāt tas pasargā no cherry-picking modelēšanā un tādas datu analīzes veidošanas, kas sakrīt ar pētnieka ekspektāciju, nenodrošinot noturību pret argumentētu kritiku.
Code
# libs
if(!require(usdm)) {install.packages("usdm"); require(usdm)}
if(!require(tidyverse)) {install.packages("tidyverse"); require(tidyverse)}
if(!require(terra)) {install.packages("terra"); require(terra)}
if(!require(readxl)) {install.packages("readxl"); require(readxl)}
if(!require(openxlsx)) {install.packages("openxlsx"); require(openxlsx)}
if(!require(doParallel)) {install.packages("doParallel"); require(doParallel)}
if(!require(foreach)) {install.packages("foreach"); require(foreach)}
# EGVs ----
faili=data.frame(fails=list.files(path="./Rastri_100m/Scaled/",
pattern=".tif$"),
cels=list.files(path="./Rastri_100m/Scaled/",
pattern=".tif$",full.names = TRUE))
# sugam paredzetie ----
sakumam=read_excel("./Rastri_100m/EGV_putniem.xlsx")
sakumam_long=sakumam %>%
pivot_longer(cols = COTCOT:EMBCIT,names_to="suga_kods",values_to="sakuma_izvele")
# Izvēle ----
sugas=levels(factor(sakumam_long$suga_kods))
cl <- makeCluster(8)
registerDoParallel(cl)
foreach(i = 1:length(sugas)) %dopar% {
suppressPackageStartupMessages(library(tidyverse))
suppressPackageStartupMessages(library(terra))
suppressPackageStartupMessages(library(arrow))
suppressPackageStartupMessages(library(usdm))
suppressPackageStartupMessages(library(maps))
suppressPackageStartupMessages(library(rasterVis))
suppressPackageStartupMessages(library(readxl))
suppressPackageStartupMessages(library(SDMtune))
suppressPackageStartupMessages(library(ENMeval))
suppressPackageStartupMessages(library(zeallot))
suppressPackageStartupMessages(library(openxlsx))
print(i)
sakums=Sys.time()
suga=sugas[i]
print(suga)
sakumsaraksts_sugai=sakumam_long %>%
filter(suga_kods==suga)
isssakums_sugai=sakumsaraksts_sugai %>%
filter(sakuma_izvele==1)
faili_sugai=faili %>%
filter(fails %in% isssakums_sugai$scale_NAME)
rastri_sugai=terra::rast(faili_sugai$cels)
VifStep_sugai=usdm::vifstep(rastri_sugai,th=10,size=20000)
izslegt=VifStep_sugai@excluded
saglabat=VifStep_sugai@results
saglabat2=saglabat %>%
mutate(faila_nosaukums=paste0(Variables,".tif"),
sakumVIF=VIF) %>%
dplyr::select(faila_nosaukums,sakumVIF)
sakums2=sakumsaraksts_sugai %>%
left_join(saglabat2,by=c("scale_NAME"="faila_nosaukums"))
EGVtabulai=paste0("./SuguModeli/EGVselection/EGV_",suga,".xlsx")
write.xlsx(sakums2,EGVtabulai)
beigas=Sys.time()
ilgums=beigas-sakums
print(ilgums)
}
stopCluster(cl)7.1.2 EGV indikatīvā nozīme kompleksā modelī
Pēc iepriekšējā soļa veikšanas (Multikolinearitāte), daļai sugu saglabājās sevišķi liels EGV loks, no kurām skaidrs, ka ne visas faktiski saistīsies ar sugas izplatību statistiskajā modelī, turklāt ir risks, ka ar regresoriem pārsātinātā informācijas telpā, daļa nozīmīgo efektu tiks nomākti, nemaz nerunājot par identificējamības ierobežojumiem sugām ar nelielu klātbūtnes vietu skaitu. Turklāt, modelēšana ar lielu regresoru skaitu ir skaitļošanas izmaksu prasīga (mērogojumam - viena “pilnā modeļa” pazīmju nozīmes izvērtējums ar deviņām permutācijām prasa vairāk laika un operatīvās atmiņas, nekā 99 permutācijas beigu modelim).
Tādēļ pirms sugas izplatības modeļu parametrizācijas, veidots indikatīvais modelis, no kura izslēgtas maznozīmīgās pazīmes. Šis modelis veidots ar visiem savstarpēji pietiekoši neatkarīgajiem EGV (Multikolinearitāte) un visiem modeļa apamācībā izmantojamajiem punktiem (klātbūtnes un fona - Modelēšanas datu saglabāšana un procesa vizualizēšana) maksimuma entropijas analīzes “noklusējuma” modelī - lineāro (linear; R funkcijās “l” vai “L”), kvadrātisko (quadratic; R funkcijās “q” vai “Q”), zemākā sliekšņa līmeņa kritērija (hinge; R funkcijās “h” vai “H”) un to produkta (product; R funkcijās “p” vai “P”) algoritmu kombinācijai ar regularizācijas multiplikatoru “1” (Phillips et al., 2004), (Phillips et al., 2006). Šis ir samērā komplekss modelis, kurš tiecās izmantot plašu pazīmju klāstu, veidojot korelatīvas saistības, kuras ļauj identificēt ietekmīgākos EGV pārējo izslēgšanai jeb modeļa reducēšanai (Phillips et al., 2006), (Björklund et al., 2020).
No izmantotajām pazīmju-algoritmu kombinācijām zemākā sliekšņa līmeņa kritērijs, lai gan ekoloģiski pamatots dažādās situācijās, {maxnet} pakotnē (Phillips, 2021) ir lietojams tikai EGV inofrmācijas telpā, kurā ik pazīmei ir pietiekoša variabilitāte, kas ne vienmēr izpildās. Tādēļ šajā solī iestrādāta automātiska izvēle nedaudz vienkāršākam modelim - LQP -, ja neizpildās variabilitātes nosacījumi. Sākotnējais modelis veidots un EGV indikatīvā nozīme vērtēta, procesa vadībai izmantojot R pakotni {SDMtune} (Vignali et al., 2020).
Visi modeļi veidoti, kopējās informācijas telpas aprakstam (fona jeb background vietām) pievienojot tās klātbūtnes vietas, kuras raksturo tajos jau neesošas EGV vērtību kombinācijas (Phillips et al., 2004), (Phillips et al., 2006), lai veidotu statistisko kompleksu, kas matemātiski cieši saistās ar Puasona punktu procesu (Guisan et al., 2017), (Phillips et al., 2017).
Lai gan šī soļa mērķis ir vienkāršot modeļus, reducējot iekļauto pazīmju loku, tas tiek darīts tikai apmācību kopā un bez iekšējās validācijas (cross-validation; CV), kas rada potenciālu pārliekai pielipšanai datiem (overfitting), turklāt risku fokusam uz atsevišķām pazīmēm, tādā veidā zaudējot matricas heterogenitātes ietekmes raksturojumus. Tādēļ iestrādāts kritērijs par minimālo pazīmju skaitu sākotnējā modelī, tam izmantojot indikāciju no vidējās ietekmes deviņās permutācijās:
ja vidējā indikatīvā ietekme bija vismaz 1% un pazīmju skaits bija vismaz 16, izvēlētas šīs pazīmes un izvēle beigta. Ja pazīmju skaits bija mazāks, turpināta izvēle;
turpinot izvēli, izvērtēts pazīmju ar vismaz 0.5% indikatīvo ietekmi. Ja tas ir vismaz 16, izvēlētas šīs pazīmes un izvēle beigta. Ja pazīmju skaits bija mazāks, turpināta izvēle;
turpinot izvēli, izmantotas pazīmes ar vismaz 0.1% indikatīvo ietekmi un izvēle beigta.
Sliekšņa līmenis ar vismaz 16 EGV ir izvēlēts arbitrāri. Skaidrs, ka optimālais EGV skaits ir pakārtots gan sugas ekoloģiskās nišas sarežģītībai, gan pieejamo vides raksturojumu detalizācijai, gan klātbūtnes vietu skaitam (Guisan et al., 2017). Tomēr sugām ar mazāku novērojumu skaitu ir augstāka varbūtība modelim pielipt kādām no konkrētām situācijām (to raksturojumiem EGV informācijas telpā). Apskatot visu modelēšanā iekļauto sugu klātbūtnes vietu apmācību kopā skaitu saistībā ar izvēlēto EGV skaitu, šī vērtība (“16”) iezīmējas gan sugām ar lielu, gan vidēju novērojumu skaitu (7.1 att.).
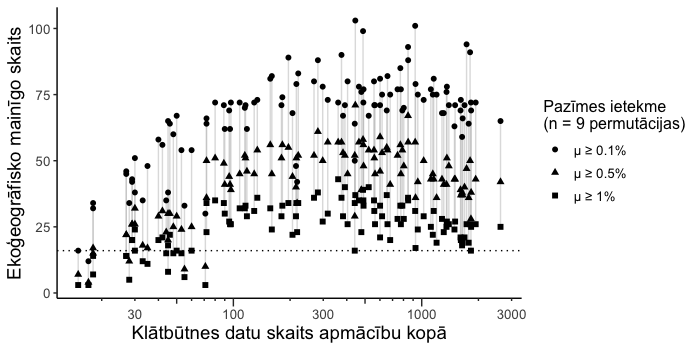
Figure 7.1: Sugu izplatības modeļu parametrizācijai izvēlāmo ekoģeogrāfisko mainīgo skaits, atkarībā no klātbūtnes datu skaita modeļa apmācību kopā un indikatīvās permutāciju ietekmes.
Procedurā ir atkārtoja ar sekojošajā koda apgabalā sniegtajām komandu rindām. To ietvaros tiek veiktas augstāk aprakstītās darbības un iepriekš (Multikolinearitāte) sagatavotajos sugām specifiskajos EGV izvēles failos pierakstīta indikatīvā nozīme kā vidējais aritmētiskais un standartnovirze permutāciju procedūrā. Turpinājumā atlasītas sliekšņa līmeņiem (EGV skaitam un vidējais ietekmei) atbilstošās pazīmes, kurām vēlreiz aprēķināta VIF vērtība, sekojot iepriekšējai procedūrai. Aprēķini atkārtoti, lai precīzāk informētu par statistisko kompleksu parametrizētajos modeļos.
Code
# libs
if(!require(usdm)) {install.packages("usdm"); require(usdm)}
if(!require(tidyverse)) {install.packages("tidyverse"); require(tidyverse)}
if(!require(terra)) {install.packages("terra"); require(terra)}
if(!require(readxl)) {install.packages("readxl"); require(readxl)}
if(!require(openxlsx)) {install.packages("openxlsx"); require(openxlsx)}
if(!require(doParallel)) {install.packages("doParallel"); require(doParallel)}
if(!require(foreach)) {install.packages("foreach"); require(foreach)}
if(!require(arrow)) {install.packages("arrow"); require(arrow)}
if(!require(maps)) {install.packages("maps"); require(maps)}
if(!require(rasterVis)) {install.packages("rasterVis"); require(rasterVis)}
if(!require(SDMtune)) {install.packages("SDMtune"); require(SDMtune)}
if(!require(ENMeval)) {install.packages("ENMeval"); require(ENMeval)}
if(!require(zeallot)) {install.packages("zeallot"); require(zeallot)}
# EGVs
egv_faili=data.frame(egv_fails=list.files(path="./Rastri_100m/Scaled/",
pattern=".tif$"),
egv_cels=list.files(path="./Rastri_100m/Scaled/",
pattern=".tif$",full.names = TRUE))
# sugas
klatbutnem=data.frame(klatbunes_fails=list.files(path="./SuguModeli/ApmacibuDati/TrainingPresence/",
pattern=".parquet"),
klatbunes_cels=list.files(path="./SuguModeli/ApmacibuDati/TrainingPresence/",
pattern=".parquet",full.names = TRUE))
klatbutnem=klatbutnem %>%
separate(klatbunes_fails,into=c("veids","kods","paplasinajums"),remove = FALSE) %>%
dplyr::select(-paplasinajums,-veids)
foniem=data.frame(fona_fails=list.files(path="./SuguModeli/ApmacibuDati/TrainingBackground/",
pattern=".parquet"),
fona_cels=list.files(path="./SuguModeli/ApmacibuDati/TrainingBackground/",
pattern=".parquet",full.names = TRUE))
foniem=foniem %>%
separate(fona_fails,into=c("veids","kods","paplasinajums"),remove = FALSE) %>%
dplyr::select(-paplasinajums,-veids)
egv_izvelem=data.frame(izvelu_fails=list.files(path="./SuguModeli/EGVselection/",
pattern=".xlsx"),
izvelu_cels=list.files(path="./SuguModeli/EGVselection/",
pattern=".xlsx",full.names = TRUE))
egv_izvelem=egv_izvelem %>%
separate(izvelu_fails,into=c("veids","kods","paplasinajums"),remove = FALSE) %>%
dplyr::select(-paplasinajums,-veids)
savienoti=klatbutnem %>%
left_join(foniem,by="kods") %>%
left_join(egv_izvelem,by="kods")
# izvēles
kodi=levels(factor(savienoti$kods))
cl <- makeCluster(6)
registerDoParallel(cl)
foreach(i = 1:length(kodi)) %dopar% {
suppressPackageStartupMessages(library(tidyverse))
suppressPackageStartupMessages(library(terra))
suppressPackageStartupMessages(library(arrow))
suppressPackageStartupMessages(library(usdm))
suppressPackageStartupMessages(library(maps))
suppressPackageStartupMessages(library(rasterVis))
suppressPackageStartupMessages(library(readxl))
suppressPackageStartupMessages(library(SDMtune))
suppressPackageStartupMessages(library(ENMeval))
suppressPackageStartupMessages(library(zeallot))
suppressPackageStartupMessages(library(openxlsx))
suga=kodi[i]
izvelei_sugai=read_excel(savienoti$izvelu_cels[savienoti$kods==suga])
izvelei_sugai=izvelei_sugai %>%
dplyr::select(sakums:sakumVIF)
isais_saraksts=izvelei_sugai %>%
filter(!is.na(sakumVIF))
egv_faili2=isais_saraksts %>%
left_join(egv_faili,by=c("scale_NAME"="egv_fails"))
predictors <- terra::rast(egv_faili2$egv_cels)
names(predictors)=egv_faili2$egv_id
names(predictors)
klatbutnem=read_parquet(savienoti$klatbunes_cels[savienoti$kods==suga])
klatbutnes=klatbutnem %>%
mutate(y=as.numeric(y)) %>%
dplyr::select(x,y)
foniem=read_parquet(savienoti$fona_cels[savienoti$kods==suga])
foni=foniem %>%
dplyr::select(x,y)
dati <- prepareSWD(species = suga,
p = klatbutnes,
a = foni,
env = predictors)
dati2=addSamplesToBg(dati)
izveles_modelis=function(datini){
rezA=try(train("Maxnet",
data = datini,
fc="lqph"))
if (inherits(rezA, 'try-error')) {
rezB=train("Maxnet",
data = datini,
fc="lqp")
return(rezB)
}
return(rezA)
}
maxnet_model=izveles_modelis(dati2)
vi_maxnet <- varImp(maxnet_model,
permut = 9)
names(vi_maxnet)=c("egv_id","first_VarImp","first_VarImpSD")
vidus=izvelei_sugai %>%
left_join(vi_maxnet,by="egv_id")
write.xlsx(vidus,savienoti$izvelu_cels[savienoti$kods==suga])
summa1=sum(ifelse(vidus$first_VarImp>=1,1,0),na.rm=TRUE)
summa05=sum(ifelse(vidus$first_VarImp>=0.5,1,0),na.rm=TRUE)
summa01=sum(ifelse(vidus$first_VarImp>=0.1,1,0),na.rm=TRUE)
if(summa1>=16) {
beigu_saraksts=vidus %>%
filter(first_VarImp>=1)} else if (summa05>=16) {
beigu_saraksts=vidus %>%
filter(first_VarImp>=0.5)} else {
beigu_saraksts=vidus %>%
filter(first_VarImp>=0.1)}
egv_faili3=beigu_saraksts %>%
left_join(egv_faili,by=c("scale_NAME"="egv_fails"))
egvs <- terra::rast(egv_faili3$egv_cels)
names(egvs)=egv_faili3$egv_id
names(egvs)
vertibam=usdm::vif(egvs,size=20000)
names(vertibam)=c("egv_id","final_VIF")
beigas=vidus %>%
left_join(vertibam,by="egv_id")
write.xlsx(beigas,savienoti$izvelu_cels[savienoti$kods==suga])
}
stopCluster(cl)7.2 Modeļa parametrizācija, izvēle un izvērtēšanas apraksti
Sugas izplatības modeļi veidoti maksimuma entropijas anlīzes ietvarā (Phillips et al., 2004), (Phillips et al., 2006), izmantojot {maxnet} pakotni (Phillips, 2021), kas vadīta ar {SDMtune} pakotni (Vignali et al., 2020). Modeļu apmācībai izmantotas tam atlasītās sugu klātbūtnes vietas un 20 000 nejauši izvēlētu fona punktu, savukārt to neatkarīgai testēšanai - atsevišķi modelī ne reizi neiekļauti neatkarīgās testēšanas dati (to izvēles apraksts - Modelēšanas datu saglabāšana un procesa vizualizēšana). No visiem pieejamajiem klātbūtnes punktiem 25% (noapaļojot uz augšu) izmantoti neatkarīgajai testēšanai, atlikušie - modeļa apmācībai. Fona jeb vides kopumā raksturošanai sākotnēji izlozēti 27500 punkti, no kuriem 7500 iekļauti neatkarīgās testēšanas kopā, pārējos izmanttojot modeļa apmācībai. Izņēmums ir vistu vanags, kuram neatkarīgās testēšanas klātbūtnes vietām izmantoti 2024. gada lauka darbu rezultāti (Modelēšanas datu saglabāšana un procesa vizualizēšana).
Sugu izplatības modelēšanā ar klātbūtnes-fona vietām, nozīmīgs izaicinājums ir klātbūtnes vietu reprezentativitāte. Optimālā situācijā, būtu jābūt pieejamai informācijai par sugu meklēšanas piepūli (Miroslav Dudik et al., 2009), (Fourcade et al., 2014), (Johnston et al., 2020), (Backstrom et al., 2024), kurai būtu jābūt iegūtai un aprakstītai tā, lai varētu izmantot nepilnīgas konstatēšanas modeļus (Kéry and Royle, 2017), (Kéry and Royle, 2021) vai integrētās pieejas (Dorazio, 2014), (Fletcher et al., 2019), (Ogawa et al., 2024). Tomēr pilnvērtīgā formā - iegūta statistiski robustas paraugošanas ietvarā un detalizēti aprakstīta - tā nav pieejama gandrīz nevienai sugai, jo konvencionālo monitoringu programmas, kurās tāda tiek iegūta, šobrīd nspēj radīt tādu informācijas bagātību, lai detalizēti analizētu visu sugu loku, turklāt nav sagaidāms, ka ar šīm metodēm būtu iespējams izstrādāt vienotu analīzes plūsmu, nodrošinot ērtu replicējamību. Šādās situācijās, simulāciju eksperimentos un reālās vides datu pētījumos ir noskaidrots, ka, ja nav iespējams nodrošināt uzticamu piepūles telpisko raksturojumu (biasfile) (Miroslav Dudik et al., 2009), (Johnston et al., 2020), pieeja ar augstāko stabilitāti pārparaugošanas (oversampling) ietekmju samazināšanā modeļa rezultātu projekcijā un pazīmju atbildes funkcijās ir sistemātiska retināšana (Fourcade et al., 2014).
Sistemātiska retināšana par faktoru 10 (nodelēšana norisinās rastra šūnā ar malas garumu 100 m, bet modeļa apmācībai izmantots tikai viens novērojums tīklā ar malas garumu 1 km) ir iestrādāta Novērojumu atlase beigās. Šāda retināša ir nozīmīga ne tikai pārparaugošanas ietekmes mazināšanai, tā spēlē arī nozīmīgu lomu maza mēroga telpiskās autokorelācijas ietekmju mazināšanā (Moudrý et al., 2024). Savukārt plaša mēroga autokorālcijas ietekmju samazināšanai un apmācītā modeļa stabilitātes novērtēšanai, izmantojama iekšējā krosvalidācija (cross-validation, CV).
Dažādos pētījumos ir noskaidrots, ka sugu izplatības modeļi var gan uzrādīt ciešu saistību ar pazīmēm, kas tikai nejauši vai ļoti netieši ir saistītas ar sugu izplatību (Dormann et al., 2012), gan nejauši ģenerētām vērtībām (Bahn and Mcgill, 2007), (Beale et al., 2008), (Chapman, 2010), gan pat renesances gleznojumiem (Fourcade et al., 2018). Tas nozīmē, ka modeļu izveides un izvērtēšanas procedūrām ir liela nozīme, lai samazinātu šādu nejaušību ietekmi. Cik tas attiecas uz plaša mēroga autokorelācijām, kas sevišķi izteiktas saistībā ar klimatu un raksturīgas renesances gleznojumos, telpisko bloku krosvalidācija ir atzīta par labāk performējošo, jo sevišķi, ja apvienota ar neatkarīgas testēšanas datiem (Veloz, 2009), (Wenger and Olden, 2012), (Roberts et al., 2017), (Fourcade et al., 2018). Šī procedūra - telpisko bloku krosvalidācija un modeļa izvērtēšana neatkarīgos testa datos - ir ieviesta šajā materiālā.
Ir neapšaubāmi skaidrs, ka neviens viens mērs nav spējīgs pilnvērtīgi raksturot sugu izplatības modeli. Tāpat arī ir skaidrs, ka nevienas programmas vai modelēšanas pieejas noklusējuma uzstādījumu, lai cik kalibrēti, nav piemēroti visām situācijām. Attiecībā uz maksimuma entropijas analīzi, kas ir kļuvusi par vienu no populārākajām sugu izplatības modelēšanas pieejām, plaši izmantota nekorekta prakse ir izmantot noklusējuma algoritmus ar noklusējuma regularizāciju un modeļa spēju raksturot ar AUC (Area Under receiver operating Curve) (Warren and Seifert, 2011), (Radosavljevic and Anderson, 2014). Šī prakse ir nekorekta, jo reti, kad atgriež konkrētās sugas izplatību vai tās ekoloģisko nišu konkrētā pētījuma teriotrijā labāk raksturojošo un labāk vispārinošo modeli (Warren and Seifert, 2011), turklāt AUC kā metrika ir daudz pamatoti kritizēta, tostarp tās tieksmes augstāk vērtēt pārpielāgotus modeļus dēļ (Lobo et al., 2008), (Warren and Seifert, 2011). Tomēr nevar noliegt tā piemērotību, piemēram, telpiski krosvalidētu modeļu daļu stabilitātes novērtēšanā (Radosavljevic and Anderson, 2014). Kā alternatīva ir ietekts izlases apjomam koriģētais Akaike informācijas kritērijs (Warren and Seifert, 2011), kura aprēķināšai izstrādāta gan patstāvīga (Warren et al., 2010), gan R vadāma programmatūra (Warren et al., 2021), (Warren and Dinnage, 2024). Tomēr arī šī metrika ir saņēmusi kritiku, gan tās aprēķināšanai nepieciešamo skaitļošanas resursu un datu apjoma dēļ, gan informācijas kritēriju parsimoniskās dabas, gan ģeogrāfiski vispārinātās projekcijas akurātuma dēļ, starp citiem apsvērumiem (Velasco and González-Salazar, 2019). Par šobrīd izplatītāko labākā modeļa izvēles pieeju ir kļuvusi TSS (patiesās spējas statisktika, True Skill Statistic), kas ir orientēta klasifikācijas spējas novērtējumā un tam izmanto informāciju gan par sensitivitāti, gan specifiskumu (Allouche et al., 2006). Šī metrika ir plaši izmantota labākās modeļa parametrizācijas izvēlei dažādos statistiskajos kompleksos un, ja labākais modelis ir vērtēts pēc tā TSS neatkarīgos testa datos, ir uzskatāms, ka tā raksturo pietuvinātu rezultātu dabā sagaidāmajam caur pārceļamību (transferability) (Wenger and Olden, 2012), (Wright et al., 2014), (Soley-Guardia et al., 2019). Tomēr arī tā nav visaptveroša pati par sevi un ir nepieciešami papildus raksturojumi un izvērtējumi.
Šajā materiālā izmantoju četru telpisko bloku krosvalidāciju, kuras ietvaros izvērtēju TSS, gan modeļa apmācības, gan validācijas kopā un pēc visu modeļa variantu sagatavošanas, arī neatkarīgos testa datos. Neatkarīgos testa datos aprēķināju arī AUC vērtību modeļu papildus raksturošanai. Modeļu veidošanā izmantoju režģa pieeju labākās parametrizācijas noskaidrošanai:
izmēģināju regularizācijas multiplikatora vērtības 0.2, 1/3, 0.5, 0.75, 1, 1.25, 2, 3, 5, 7.5 un 10;
sekojošus algoritmus:
visām sugām tika izmēģināta algoritmu “l”, “lq”, “lp”, “lqp”, “qp”, “lh”, “qh”, “lqh”, “lhp”, “qhp” un “lqhp” kopa, tomēr ne visām tā bija iespēja EGV vērtību variabilitātes dēļ, tādēļ pēc kļūdas paziņojuma automātiski ieviesta cita algoritmu kopa;
pēc kļūdas paziņojuma 2.a algoritmiem, izmēģināta “l”, “lq”, “lp”, “lqp”, “qp” un “q” kopa, kas vienai sugai nišas kompleksitātes dēļ nespēja konverģēt;
vienai sugai pēc konverģences kļūdām 2.b algoritmu kopā ieviesta “l”, “lq” un “q” kopa.
Tas nozīmē, ka ik sugai izmēģināts relatīvi liels apjoms modeļu:
2.a gadījumā tā ir 121 parametrizācija, kas ieviesta četros telpiskajos blokos, veidojot 484 modeļus. Katrai no 121 parametrizācijas izveidots krosvalidāciju kombinētais modelis, kurš atkārtoti pielāgots un izvērtēts neatkarīgās testēšanas kopā, kas nozīmē vēl 121 modeļa gatavošanu;
2.b gadījumā tās ir 66 parametrizācijas, kas ieviestas četros telpiskajos blokos, veidojot 264 modeļus. Katrai no 66 parametrizācijām izveidots krosvalidāciju kombinētais modelis, kurš atkārtoti pielāgots un izvērtēts neatkarīgās testēšanas kopā, kas nozīmē vēl 66 modeļu gatavošanu;
2.c gadījumā tās ir 33 parametrizācijas, kas ieviestas četros telpiskajos blokos, veidojot 132 modeļus. Katrai no 33 parametrizācijām izveidots krosvalidāciju kombinētais modelis, kurš atkārtoti pielāgots un izvērtēts neatkarīgās testēšanas kopā, kas nozīmē vēl 33 modeļu gatavošanu.
Visi modeļi sagatavoti, limitējot atbildes funkcijas telpai, kas raksturota ar vērtībām modeļa apmācībā izmantotajos klātbūtnes un fona punktos. Ārpus šo vērtību apgabala projicētā dzīvotņu piemērotība limitēta ekspektācijai pie EGV kombināciju vērtību robežām (Phillips et al., 2004), (Phillips et al., 2006), (Miroslav Dudik et al., 2009), (Phillips et al., 2017).
Ik sugai kā R objekts saglabāts gan viss izveidoto modeļu loks, gan par labāko atzītais modelis - gan kā telpisko bloku krosvalidāciju, gan to apvienojuma objekts, un, protams, parametrizāciju raksturojuma tabula labākās izvēlei. Par labāko parametrizāciju (sugas izplatības modeli) atzīts tas, ar augstāko TSS neatkarīgās testēšanas datos. Ja vairākiem modeļiem tā bija vienāda, tad tas ar mazāko starpību validācijas un apmācības datu kopās (labāko vispārināšanās spēju un mazāko pārpielāgošanu). Ja šie kritēriji atgrieza vairākus modeļus, izvēlēts tas ar augstāko validācijas TSS un izvēle, tās turpināšanas gadījumā, noslēgta ar parametrizāciju, kurai ir vienkāršākā algoritmu kombinācija.
Par labāko atzītajam modelim:
sagatavota cloglog tranformēta dzīvotņu piemērotības projekcija (Phillips et al., 2017) kā GeoTIFF fails;
Excel failā piedāvāti biežākie sliekšņa līmeņi dzīvotņu piemērotības binārai klasifikācijai piemērotās un nepiemērotās ar kļūdu matricas raksturojumu un statistiskā nozīmīguma līmeni klasifikācijai (salīdzinājumā ar nejaušu līdzvērtīga apjoma telpas izlozi);
R objektā saglabāts attēls ar AUC līkni plašākai vērtēšanai;
labākajam modelim (kā krosvalidāciju objektam, lai labāk novērtētu stabilitāti) sagatavots pazīmju ietekmes novērtējums 99 permutāciju procedūrā, kura vērtības (vidējais aritmēriskais un standartnovirze) saglabātas excel failos ar sugai specifisko EGV izvēles gaitu.
Par labāko atzītais modelis tālāk nodots detalizētai vērtēšanai dažādos salīdzinājumos ar nejaušību, kas ģenerēta tieši sugai specifisko EGV informācijas telpā - Nulles modelis.
Sekojošajā koda apgabalā ir sniegtas izmantotās komandu rindas.
Code
suga="abcdef" # sugas sešu burtu kods
# viss sekojošais, protams, ir ieliekams ciklā, kura vadībai izmantojams sugas kods,
# tomēr ir jārēķinās, ka ik vienas sugas SDM parametrizācija aizņem no dažām stundām
# līdz pāris diennaktīm, pieprasot starp 20 un 200 GB operatīvās atmiņas. Šī nevienmērība
# nepieļauj īsti labu uzdevuma sagatavošanu, tādēļ šī materiāla tapšanas laikā SDM
# parametrizācija veidota sugai-specifisku uzdevumu veidā HPC, paredzot ik sugai
# individuālu resursu pieprasīšanu (sākot no 20 GB RAM, to iteratīvi palielinot
# par 10 GB līdz ar katru nepietiekama operatīvās atmiņas apjoma dēļ pārtrauktu
# uzdevuma izpildi)
# pakotnes darbam
suppressPackageStartupMessages(library(plotROC))
suppressPackageStartupMessages(library(ecospat))
suppressPackageStartupMessages(library(maxnet))
suppressPackageStartupMessages(library(tidyverse))
suppressPackageStartupMessages(library(terra))
suppressPackageStartupMessages(library(arrow))
suppressPackageStartupMessages(library(usdm))
suppressPackageStartupMessages(library(maps))
suppressPackageStartupMessages(library(rasterVis))
suppressPackageStartupMessages(library(readxl))
suppressPackageStartupMessages(library(SDMtune))
suppressPackageStartupMessages(library(ENMeval))
suppressPackageStartupMessages(library(zeallot))
suppressPackageStartupMessages(library(openxlsx))
# vadibas faili
print(paste0("Ielasu un sagatavoju datus: ",Sys.time()))
PresTrain=data.frame(PresTrain_fails=list.files(path="./SuguModeli/ApmacibuDati/TrainingPresence/",
pattern=".parquet"),
PresTrain_cels=list.files(path="./SuguModeli/ApmacibuDati/TrainingPresence/",
pattern=".parquet",full.names = TRUE))
PresTrain=PresTrain %>%
separate(PresTrain_fails,into=c("veids","kods","paplasinajums"),remove = FALSE) %>%
dplyr::select(-paplasinajums,-veids)
BgTrain=data.frame(BgTrain_fails=list.files(path="./SuguModeli/ApmacibuDati/TrainingBackground/",
pattern=".parquet"),
BgTrain_cels=list.files(path="./SuguModeli/ApmacibuDati/TrainingBackground/",
pattern=".parquet",full.names = TRUE))
BgTrain=BgTrain %>%
separate(BgTrain_fails,into=c("veids","kods","paplasinajums"),remove = FALSE) %>%
dplyr::select(-paplasinajums,-veids)
PresTest=data.frame(PresTest_fails=list.files(path="./SuguModeli/ApmacibuDati/TestingPresence/",
pattern=".parquet"),
PresTest_cels=list.files(path="./SuguModeli/ApmacibuDati/TestingPresence/",
pattern=".parquet",full.names = TRUE))
PresTest=PresTest %>%
separate(PresTest_fails,into=c("veids","kods","paplasinajums"),remove = FALSE) %>%
dplyr::select(-paplasinajums,-veids)
BgTest=data.frame(BgTest_fails=list.files(path="./SuguModeli/ApmacibuDati/TestingBackground/",
pattern=".parquet"),
BgTest_cels=list.files(path="./SuguModeli/ApmacibuDati/TestingBackground/",
pattern=".parquet",full.names = TRUE))
BgTest=BgTest %>%
separate(BgTest_fails,into=c("veids","kods","paplasinajums"),remove = FALSE) %>%
dplyr::select(-paplasinajums,-veids)
egv_izvelem=data.frame(izvelu_fails=list.files(path="./SuguModeli/EGVselection/",
pattern=".xlsx"),
izvelu_cels=list.files(path="./SuguModeli/EGVselection/",
pattern=".xlsx",full.names = TRUE))
egv_izvelem=egv_izvelem %>%
separate(izvelu_fails,into=c("veids","kods","paplasinajums"),remove = FALSE) %>%
dplyr::select(-paplasinajums,-veids)
savienoti=PresTrain %>%
left_join(BgTrain,by="kods") %>%
left_join(PresTest,by="kods") %>%
left_join(BgTest,by="kods") %>%
left_join(egv_izvelem,by="kods")
savsugai=savienoti %>%
filter(kods==suga)
# egvs
egv_faili=data.frame(egv_fails=list.files(path="./Rastri_100m/Scaled/",
pattern=".tif$"),
egv_cels=list.files(path="./Rastri_100m/Scaled/",
pattern=".tif$",full.names = TRUE))
egv_izvelei=read_excel(savsugai$izvelu_cels)
egv_izvelei2=egv_izvelei %>%
filter(!is.na(final_VIF))
egv_faili=egv_faili %>%
right_join(egv_izvelei2,by=c("egv_fails"="scale_NAME"))
egvs=terra::rast(egv_faili$egv_cels)
names(egvs)=egv_faili$egv_id
# apmācību dati
treninklatbutnes=read_parquet(savsugai$PresTrain_cels)
treninklatbutnes=treninklatbutnes %>%
mutate(y=as.numeric(y)) %>%
dplyr::select(x,y)
treninfons=read_parquet(savsugai$BgTrain_cels)
treninfons=treninfons %>%
mutate(y=as.numeric(y)) %>%
dplyr::select(x,y)
trenin_dati <- prepareSWD(species = suga,
p = treninklatbutnes,
a = treninfons,
env = egvs)
trenin_dati=addSamplesToBg(trenin_dati)
block_folds <- get.block(occ = trenin_dati@coords[trenin_dati@pa == 1, ],
bg = trenin_dati@coords[trenin_dati@pa == 0, ])
# testa dati
testklatbutnes=read_parquet(savsugai$PresTest_cels)
testklatbutnes=testklatbutnes %>%
ungroup() %>%
mutate(y=as.numeric(y)) %>%
dplyr::select(x,y)
testfons=read_parquet(savsugai$BgTest_cels)
testfons=testfons %>%
mutate(y=as.numeric(y)) %>%
dplyr::select(x,y)
testa_dati=prepareSWD(species=suga,
p = testklatbutnes,
a = testfons,
env = egvs)
rm(treninklatbutnes)
rm(treninfons)
rm(testklatbutnes)
rm(testfons)
rm(BgTest)
rm(BgTrain)
rm(PresTest)
rm(PresTrain)
rm(egv_izvelem)
# Grid Search
print(paste0("Uzsāku modelēšanu: ",Sys.time()))
sakummodelis <- train(method = "Maxnet",
data = trenin_dati,
test=testa_dati,
fc="lq",
folds = block_folds)
print(paste0("Uzsāku grid search: ",Sys.time()))
# burtu secībai ir nozīme!
fc_lqph <- list(reg = c(0.2, 1/3, 0.5, 0.75, 1, 1.25, 2, 3, 5, 7.5, 10),
fc = c("l", "lq", "lp", "lqp", "qp","lh","qh","lqh","lhp","qhp","lqhp"))
fc_lqp <- list(reg = c(0.2, 1/3, 0.5, 0.75, 1, 1.25, 2, 3, 5, 7.5, 10),
fc = c("l", "lq", "lp", "lqp", "qp","q"))
fc_lq <- list(reg = c(0.2, 1/3, 0.5, 0.75, 1, 1.25, 2, 3, 5, 7.5, 10),
fc = c("l", "lq", "q"))
izveles_rezgis <- function(objekts) {
rezA <- try(gridSearch(objekts,
hypers = fc_lqph,
metric = "tss"), silent = TRUE)
if (inherits(rezA, 'try-error')) {
rezB <- try(gridSearch(objekts,
hypers = fc_lqp,
metric = "tss"), silent = TRUE)
if (inherits(rezB, 'try-error')) {
rezC <- gridSearch(objekts,
hypers = fc_lq,
metric = "tss")
return(rezC)
}
return(rezB)
}
return(rezA)
}
meklesanas_rezgis <- izveles_rezgis(sakummodelis)
write_rds(meklesanas_rezgis,paste0("./SuguModeli/GridSearch_Models/GSModeli_",suga,".RDS"))
rm(sakummodelis)
# izveles tabula
print(paste0("Uzsāku izvēles tabulu: ",Sys.time()))
izveles_tabula=meklesanas_rezgis@results
izveles_tabula$IndepTest_auc=NA_real_
izveles_tabula$IndepTest_tss=NA_real_
darbiba_auc=function(numurs){
rez=try(auc(combineCV(meklesanas_rezgis@models[[numurs]]),test=testa_dati))
if (inherits(rez, 'try-error')) {
return(NA)
}
return(rez)
}
darbiba_tss=function(numurs){
rez=try(tss(combineCV(meklesanas_rezgis@models[[numurs]]),test=testa_dati))
if (inherits(rez, 'try-error')) {
return(NA)
}
return(rez)
}
for(i in 1:nrow(izveles_tabula)){
print(i)
fin_auc=darbiba_auc(i)
izveles_tabula$IndepTest_auc[i]=fin_auc
fin_tss=darbiba_tss(i)
izveles_tabula$IndepTest_tss[i]=fin_tss
#print(paste0("independent AUC: ",fin_auc))
#print(paste0("independent TSS: ",fin_tss))
}
names(izveles_tabula)=c("fc","reg","train_TSS","validation_TSS","diff_TSS","IndepTest_auc","IndepTest_tss")
write.xlsx(izveles_tabula,paste0("./SuguModeli/GridSearch_Tables/GSTabula_",suga,".xlsx"))
# labaka noskaidrosana
print(paste0("Izvēlos labāko: ",Sys.time()))
labakajam_modelim=izveles_tabula %>%
mutate(rinda=as.numeric(rownames(.))) %>%
filter(IndepTest_tss==max(IndepTest_tss,na.rm=TRUE)) %>%
filter(diff_TSS==min(diff_TSS,na.rm=TRUE)) %>%
filter(validation_TSS==max(validation_TSS,na.rm=TRUE)) %>%
filter(nchar(fc)==min(nchar(fc)))
labaka_numurs=labakajam_modelim$rinda
# krosvalidetais
print(paste0("Saglabāju labāko CV: ",Sys.time()))
labakais_CV=meklesanas_rezgis@models[[labaka_numurs]]
write_rds(labakais_CV,paste0("./SuguModeli/BestCV/BestCV_",suga,".RDS"))
# kombinetais
print(paste0("Saglabāju labāko kombinēto: ",Sys.time()))
labakais_comb=combineCV(meklesanas_rezgis@models[[labaka_numurs]])
write_rds(labakais_comb,paste0("./SuguModeli/BestComb/BestComb_",suga,".RDS"))
rm(meklesanas_rezgis)
# projekcija
print(paste0("Saglabāju HS projekciju: ",Sys.time()))
map_best <- predict(labakais_comb,
data = egvs,
type = "cloglog",
file = paste0("./SuguModeli/BestHSmap/BestHSmap_",suga,".tif"),
overwrite=TRUE)
#terra::plot(map_best)
rm(map_best)
# thresholds
print(paste0("Saglabāju sliekšņa līmeņus: ",Sys.time()))
ths <- SDMtune::thresholds(labakais_comb,
type = "cloglog",
test=testa_dati)
ths$suga=suga
write.xlsx(ths,paste0("./SuguModeli/BestThresholds/BestThs_",suga,".xlsx"))
rm(ths)
# pROC
print(paste0("Saglabāju ROC līkni: ",Sys.time()))
labakais_proc=SDMtune::plotROC(labakais_comb,test = testa_dati)
labakais_proc
write_rds(labakais_proc,paste0("./SuguModeli/BestROCs/BestROC_",suga,".RDS"))
rm(labakais_proc)
# var importance
print(paste0("Uzsāku egv nozīmi: ",Sys.time()))
vi_tss <- varImp(labakais_CV,permut = 99)
names(vi_tss)=c("egv_id","final_PermImp_avg","final_PermImp_sd")
egv_importance=egv_izvelei %>%
left_join(vi_tss,by="egv_id")
write.xlsx(egv_importance,paste0("./SuguModeli/BestVarImp/BestVarImp_",suga,".xlsx"))
rm(vi_tss)
rm(egv_importance)
# faktiskā sugai specifiskā uzdevuma izpildē HPC, komandu rindas turpinās ar nākošo koda apgabalu7.3 Nulles modelis
Tā kā vēl joprojām zinātnē nav īstas skaidrības par sugu izplatības modeļu (un kopumā dažādu vispārināto modeļu) kvalitātes un uzticamības raksturojumu patiesumu, jo sevišķi klātbūtnes-fona modeļos, ir introducēta nulles modeļu pieeja. Šīs pieejas pamatā ir dažādu raksturojumu aprēķināšana empīriskajos datos un to pašu metriku aprēķināšana nejauši ģenerētās vērtībās tajā pašā (EGV) informācijas telpā. Sākotnējās implementācijas sugu izplatības modeļos spēja empīriskās vērtības saalīdzināt ar nejauši ģenerētu vietu prognozēšanas spēju tikai, izmantojot nejaušo krosvalidāciju (Raes and Steege, 2007). Kopš tā laika ir izstrādātas pieejas neatkarīgas testēšanas datu kopas izmantošanai (Jamie M. Kass and Anderson, 2019) un telpisko bloku krosvalidācijai (Kass et al., 2020). Šīs pieejas ir ieviestas R pakotnē {ENMeval} (Kass et al., 2021) un izmantotas šajā materiālā.
Kā jau iepriekš rakstīts, sugu izplatības modeļi var nosacīti labi aprakstīties gan ar nejaušām saistībām, gan pat ar renesances glezonojumiem (skatīt nodaļā Modeļa parametrizācija, izvēle un izvērtēšanas apraksti), tādēļ saprotams, ka arī nejauši ģenerētas vietas var relatīvi labi aprakstīties. Daudzas modeļa izvērtējumos izmantotās metrikas ir klasifikācijas sliekšņa līmeņa atkarīgas, tādēļ vērtējot izstrādāto modeļu spēju salīdzinājumā ar nulles modeļiem, vēlamies redzēt, ka tiem ir labākas vērtības, tomēr par pieņemamiem modeļiem var tikt uzskatīti arī tie empīriskie modeļi, kuriem tās nav sliktākas par nulles modeļiem (Muscarella et al., 2014). Vairāk par aprēķinātajām metrikām un to interpretāciju rezultātu nodaļas Individuālu sugu rezultāti apakšnodaļā.
Empīriskā modeļa (ierpiekš par labāko atzītā) salīdzinājums ar tā EGV veidotajā informācijas telpā ģenerētiem katrai sugai 100 nulles modeļiem, ir sekojošajā koda apgabalā. Šajā materiālā tas ir nodalīts arsevišķi no iepriekšējā (Modeļa parametrizācija, izvēle un izvērtēšanas apraksti), tomēr tie ir izpildāmi kopā.
Code
# šis ir turpinājums iepriekšējam koda apgabalam un izmantojams tajā pašā uzdevumā ik sugai
# Nulles reference
print(paste0("Uzsāku nulles referenci: ",Sys.time()))
ref_fc=labakais_comb@model@fc
ref_rm=labakais_comb@model@reg
occs=trenin_dati@coords[trenin_dati@pa==1,]
bg=trenin_dati@coords[trenin_dati@pa==0,]
rm(testa_dati)
rm(trenin_dati)
rm(labakais_CV)
rm(labakais_comb)
rm(izveles_tabula)
rm(fc_lqp)
rm(fc_lqph)
rm(egv_faili)
rm(egv_izvelei)
rm(egv_izvelei2)
rm(savienoti)
rm(savsugai)
rm(labakajam_modelim)
rm(block_folds)
tune.args <- list(fc = ref_fc, rm = ref_rm)
nulles_reference <- ENMevaluate(occs = occs, envs = egvs, bg = bg,
algorithm = 'maxnet', partitions = 'block',
tune.args = tune.args)
write_rds(nulles_reference,paste0("./SuguModeli/Null_reference/NullRef_",suga,".RDS"))
# Nulles salidzinajumi
print(paste0("Uzsāku nulles salīdzinājumus: ",Sys.time()))
nulles_modeli <- ENMnulls(nulles_reference, mod.settings = list(fc = ref_fc, rm = ref_rm), no.iter = 100)
write_rds(nulles_modeli,paste0("./SuguModeli/Null_models/NullModels_",suga,".RDS"))
print(paste0("Beidzu: ",Sys.time()))7.4 Labākā modeļa rezultāti
Pēc labākā modeļa izvēles un tā salīdzinājuma ar nulles modeli, sagatavotas ilustrācijas Rezultāti nodaļai, sniedzot iespēju katram lietotājam pašam pieņemt lēmumu par kādu modeļu lietošanu konkrētiem mērķiem. Starp modeļu vērtēšanas un aprakstīšanas materiāliem, sniegti arī īsi komentāri.
Modeļu izvērtēšanai sagatavots ar visu parametrizāciju aprakstu, to raksturojot ar neatkarīgās testēšanas TSS, starpību starp validēšanas un apmācības TSS, validēšanas TSS, apmācību TSS un neatkarīgās testēšanas kopas AUC. Šim attēlam pievienots ROC līkņu attēls par labāko atzītajā modelī, kurā attēla modeļa spēja patiesi piemēroto un viltus piemēroto dzīvotņu telpā. Papildus tam, pievienots attēls ar labākākā modeļa salīdzinājumu ar nulles modeļiem, vērtējot validācijas AUC, nepārtraukti variējošo Boisa indeksu un divus apmācību kopas klātbūtnes vietu pareizas klasifikācijas rādītājus. To interpretācija raksturota nodaļas Individuālu sugu rezultāti sākumā.
Code
if(!require(tidyverse)) {install.packages("tidyverse"); require(tidyverse)}
if(!require(readxl)) {install.packages("readxl"); require(readxl)}
if(!require(terra)) {install.packages("terra"); require(terra)}
if(!require(ENMeval)) {install.packages("ENMeval"); require(ENMeval)}
if(!require(patchwork)) {install.packages("patchwork"); require(patchwork)}
if(!require(ggview)) {install.packages("ggview"); require(ggview)}
if(!require(ggtext)) {install.packages("ggtext"); require(ggtext)}
if(!require(scales)) {install.packages("scales"); require(scales)}
failiem=data.frame(faili=list.files("./SuguModeli/GridSearch_Tables/",
pattern=".xlsx"))
failiem=failiem %>%
separate(faili,into=c("sakums","kods","beigas"),remove = FALSE)
sugas=levels(factor(failiem$kods))
for(i in seq_along(sugas)){
print(i)
suga=sugas[i]
print(suga)
izveles_tabula=read_excel(paste0("./SuguModeli/GridSearch_Tables/GSTabula_",
suga,
".xlsx"))
izveles_tabula_long=izveles_tabula %>%
pivot_longer(cols=train_TSS:IndepTest_tss,
names_to = "veids",
values_to = "vertibas") %>%
mutate(veids_long=case_when(veids=="train_TSS"~"Apmācību\nTSS",
veids=="validation_TSS"~"Validācijas\nTSS",
veids=="diff_TSS"~"Apmācību un\nvalidācijas\nTSS starpība",
veids=="IndepTest_auc"~"Neatkarīgā\ntesta\nAUC",
veids=="IndepTest_tss"~"Neatkarīgā\ntesta\nTSS")) %>%
mutate(sec_veids=case_when(veids=="train_TSS"~4,
veids=="validation_TSS"~3,
veids=="diff_TSS"~2,
veids=="IndepTest_auc"~5,
veids=="IndepTest_tss"~1))
izveles_labakais=izveles_tabula %>%
mutate(rinda=as.numeric(rownames(.))) %>%
filter(IndepTest_tss==max(IndepTest_tss,na.rm=TRUE)) %>%
filter(diff_TSS==min(diff_TSS,na.rm=TRUE)) %>%
filter(validation_TSS==max(validation_TSS,na.rm=TRUE)) %>%
filter(nchar(fc)==min(nchar(fc)))
izveles_labakais_long=izveles_labakais %>%
pivot_longer(cols=train_TSS:IndepTest_tss,
names_to = "veids",
values_to = "vertibas") %>%
mutate(veids_long=case_when(veids=="train_TSS"~"Apmācību\nTSS",
veids=="validation_TSS"~"Validācijas\nTSS",
veids=="diff_TSS"~"Apmācību un\nvalidācijas\nTSS starpība",
veids=="IndepTest_auc"~"Neatkarīgā\ntesta\nAUC",
veids=="IndepTest_tss"~"Neatkarīgā\ntesta\nTSS")) %>%
mutate(sec_veids=case_when(veids=="train_TSS"~4,
veids=="validation_TSS"~3,
veids=="diff_TSS"~2,
veids=="IndepTest_auc"~5,
veids=="IndepTest_tss"~1))
# roci
rociem=read_rds(paste0("./SuguModeli/BestROCs/BestROC_",
suga,
".RDS"))
nullem=read_rds(paste0("./SuguModeli/Null_models/NullModels_",
suga,
".RDS"))
nullu_tabula_apkopots=nullem@null.emp.results
nullu_tabula_nulles=nullem@null.results
nullu_tabulai=evalplot.nulls(nullem,
stats = c("auc.val","cbi.val","or.mtp","or.10p"),
plot.type = "violin",
return.tbl = TRUE)
nulles=nullu_tabulai$null.avgs %>%
mutate(nosaukumi=case_when(metric=="auc.val"~"AUC\n(validācijas)",
metric=="cbi.val"~"Continuous\nBoyce index\n(validācijas)",
metric=="or.10p"~"10% training\nomission rate",
metric=="or.mtp"~"Minimum\ntraining presence\nomission rate")) %>%
mutate(secibai=case_when(metric=="auc.val"~1,
metric=="cbi.val"~2,
metric=="or.10p"~3,
metric=="or.mtp"~4))
empiriskie=nullu_tabulai$empirical.results %>%
mutate(nosaukumi=case_when(metric=="auc.val"~"AUC\n(validācijas)",
metric=="cbi.val"~"Continuous\nBoyce index\n(validācijas)",
metric=="or.10p"~"10% training\nomission rate",
metric=="or.mtp"~"Minimum\ntraining presence\nomission rate")) %>%
mutate(secibai=case_when(metric=="auc.val"~1,
metric=="cbi.val"~2,
metric=="or.10p"~3,
metric=="or.mtp"~4))
kreisais=ggplot()+
geom_violin(data=izveles_tabula_long,
aes(reorder(veids_long,sec_veids),vertibas),
col="grey",
fill="grey",
alpha=0.2)+
geom_jitter(data=izveles_tabula_long,
aes(reorder(veids_long,sec_veids),vertibas),
col="grey",
width=0.25)+
geom_point(data=izveles_labakais_long,
aes(reorder(veids_long,sec_veids),vertibas),
col="black",
size=3)+
theme_classic()+
coord_cartesian(ylim=c(0,1))+
scale_y_continuous(breaks=seq(0,1,by=0.1))+
labs(x="Metrika",
y="Vērtība",
subtitle="Modeļa izvēle")+
theme(axis.title = element_text(size=14),
axis.text = element_text(size=11),
plot.subtitle = element_text(size=14))
vidus=rociem+
theme_bw()+
labs(subtitle="ROC līkne")+
theme(axis.title = element_text(size=14),
axis.text = element_text(size=11),
plot.subtitle = element_text(size=14),
legend.title = element_text(size=14),
legend.text = element_text(size=11),
legend.position="inside",
legend.position.inside = c(0.8,0.15))
labais=ggplot()+
geom_violin(data=nulles,
aes(reorder(nosaukumi,secibai),avg),
col="grey",
fill="grey",
alpha=0.2)+
geom_jitter(data=nulles,
aes(reorder(nosaukumi,secibai),avg),
col="grey",
width=0.2,
shape=3)+
geom_point(data=empiriskie,
aes(reorder(nosaukumi,secibai),avg),
col="black",
size=3)+
coord_cartesian(ylim=c(0,1))+
theme_classic()+
scale_y_continuous(breaks=seq(0,1,0.1))+
labs(x="Metrika",y="Vērtība",subtitle="Izvēlētā modeļa salīdzinājums ar nejaušību")+
theme(axis.title = element_text(size=14),
axis.text = element_text(size=11),
plot.subtitle = element_text(size=14))
izveles_attelam=kreisais+vidus+labais+plot_annotation(tag_levels="A")+
ggview::canvas(width=1750,height=500,units="px",dpi=100)
izveles_attels=kreisais+vidus+labais+plot_annotation(tag_levels="A")
ggsave(izveles_attels,filename=paste0("./SuguModeli/Beigam_IzvelesAttels/IzvelesAttels_",
suga,
".png"),
width=1750,height=500,units="px",dpi=100)
}Ātram izvērtējumam, sagatavots projicētās dzīvotņu piemērotības attēls, to vizualizējot MexEnt krāsu gammā (Phillips et al., 2004), (Phillips et al., 2006), par viduspunktu nosakot vienādas sensitivitātes un specifiskuma sliekšņa līmeni. Šis sliekšņa līmenis nav piedāvāts kā obligāti labākais. Tas izvēlēts uzskatāmībai un interpretācijas ērtībai, lietotāji var izvēlēties citus, piemēram, no rezultātu nodaļā sniegtajiem vai citiem. Vairāk - Individuālu sugu rezultāti sākumā.
Code
if(!require(tidyverse)) {install.packages("tidyverse"); require(tidyverse)}
if(!require(readxl)) {install.packages("readxl"); require(readxl)}
if(!require(terra)) {install.packages("terra"); require(terra)}
if(!require(ENMeval)) {install.packages("ENMeval"); require(ENMeval)}
if(!require(patchwork)) {install.packages("patchwork"); require(patchwork)}
if(!require(ggview)) {install.packages("ggview"); require(ggview)}
if(!require(ggtext)) {install.packages("ggtext"); require(ggtext)}
if(!require(scales)) {install.packages("scales"); require(scales)}
failiem=data.frame(faili=list.files("./SuguModeli/GridSearch_Tables/",
pattern=".xlsx"))
failiem=failiem %>%
separate(faili,into=c("sakums","kods","beigas"),remove = FALSE)
sugas=levels(factor(failiem$kods))
for(i in seq_along(sugas)){
print(i)
suga=sugas[i]
print(suga)
slieksni=read_excel(paste0("./SuguModeli/BestThresholds/BestThs_",
suga,
".xlsx"))
slieksnis=slieksni[2,2]
slieksnis_vert=as.numeric(slieksnis)
apaksdala=mean(c(0,slieksnis_vert))
augsdala=mean(c(1,slieksnis_vert))
slanis=terra::rast(paste0("./SuguModeli/BestHSmap/BestHSmap_",
suga,
".tif"))
slanis_df=terra::as.data.frame(slanis,xy=TRUE)
slanis_df_augstie=slanis_df[slanis_df$lyr1>=slieksnis_vert,]
slanis_df_zemie=slanis_df[slanis_df$lyr1<slieksnis_vert,]
krasas <- c("#2c7bb6", "#abd9e9", "#ffffbf", "#fdae61", "#d7191c")
parejas <- c(0, apaksdala, slieksnis_vert, augsdala, 1)
karte=ggplot(slanis_df,aes(x=x,y=y,fill=lyr1))+
geom_raster() +
coord_fixed(ratio=1)+
scale_fill_gradientn("",
colors = krasas,
values = parejas,
breaks=c(0,round(slieksnis_vert,3),1),
limits=c(0,1))+
ggthemes::theme_map()+
theme(legend.position = "inside",
legend.position.inside=c(0,0.6),
plot.background = element_rect(fill="white",color="white"))
ggsave(karte,
filename=paste0("./SuguModeli/Beigam_KarteNebal/BeiguKarteiNebal_",
suga,
".png"),
width=900,height=550,units="px",dpi=100)
}Katrai sugai sagatavotas EGV atbildes funkcijas, raksturojot ik EGV ietekmi uz cloglog projicēto dzīvotņu piemērotību, pieņemot, ka visas pārējās pazīmes atrodas to vidējā aritmētiskajā stāvoklī.
Code
if(!require(tidyverse)) {install.packages("tidyverse"); require(tidyverse)}
if(!require(Matrix)) {install.packages("Matrix"); require(Matrix)}
if(!require(maxnet)) {install.packages("maxnet"); require(maxnet)}
if(!require(readxl)) {install.packages("readxl"); require(readxl)}
if(!require(SDMtune)) {install.packages("SDMtune"); require(SDMtune)}
if(!require(ENMeval)) {install.packages("ENMeval"); require(ENMeval)}
if(!require(ggtext)) {install.packages("ggtext"); require(ggtext)}
if(!require(usdm)) {install.packages("usdm"); require(usdm)}
if(!require(maps)) {install.packages("maps"); require(maps)}
if(!require(rasterVis)) {install.packages("rasterVis"); require(rasterVis)}
if(!require(zeallot)) {install.packages("zeallot"); require(zeallot)}
sugam=data.frame(faili=list.files("./SuguModeli/BestCV/"))
sugam=sugam %>%
separate(faili,into=c("sakums","suga","beigas"),remove = FALSE)
sugas=sugam$suga
for(j in seq_along(sugas)){
print(j)
sakums=Sys.time()
suga=sugas[j]
print(suga)
modelis_CV=read_rds(paste0("./SuguModeli/BestCV/BestCV_",suga,".RDS"))
mainigo_tabula=read_excel(paste0("./SuguModeli/BestVarImp/BestVarImp_",suga,".xlsx"))
mainigie=mainigo_tabula %>%
filter(!is.na(final_PermImp_avg))
augstums=ceiling(length(mainigie$Nosaukums)/7)*300
a=plotResponse(modelis_CV,
var = mainigie$egv_id[1],
type = "cloglog",
only_presence = TRUE,
marginal = TRUE,
rug = TRUE,
col="black")
b=ggplot2::ggplot_build(a)
saistibas_funkcija=b$plot$data
saistibas_funkcija$nosaukums=mainigie$Nosaukums[1]
saistibas_funkcija$egv=mainigie$egv_id[1]
vietas_presence=b$data[[3]]
vietas_presence$y=1
vietas_presence$nosaukums=mainigie$Nosaukums[1]
vietas_presence$egv=mainigie$egv_id[1]
vietas_absence=b$data[[4]]
vietas_absence$y=-0.03
vietas_absence$nosaukums=mainigie$Nosaukums[1]
vietas_absence$egv=mainigie$egv_id[1]
for(i in 2:length(mainigie$egv_id)){
a=plotResponse(modelis_CV,
var = mainigie$egv_id[i],
type = "cloglog",
only_presence = TRUE,
marginal = TRUE,
rug = TRUE,
col="black")
b=ggplot2::ggplot_build(a)
saistibas_funkcija_i=b$plot$data
saistibas_funkcija_i$nosaukums=mainigie$Nosaukums[i]
saistibas_funkcija_i$egv=mainigie$egv_id[i]
vietas_presence_i=b$data[[3]]
vietas_presence_i$y=1
vietas_presence_i$nosaukums=mainigie$Nosaukums[i]
vietas_presence_i$egv=mainigie$egv_id[i]
vietas_absence_i=b$data[[4]]
vietas_absence_i$y=-0.03
vietas_absence_i$nosaukums=mainigie$Nosaukums[i]
vietas_absence_i$egv=mainigie$egv_id[i]
saistibas_funkcija=bind_rows(saistibas_funkcija,saistibas_funkcija_i)
vietas_presence=bind_rows(vietas_presence,vietas_presence_i)
vietas_absence=bind_rows(vietas_absence,vietas_absence_i)
}
attels=ggplot(saistibas_funkcija)+
geom_ribbon(data=saistibas_funkcija,aes(x=x,y=y,ymin=y_min,ymax=y_max),alpha=0.5)+
geom_line(data=saistibas_funkcija,aes(x=x,y=y))+
facet_wrap(~nosaukums,scales = "free_x",ncol=7,
labeller = label_wrap_gen(width=25,multi_line = TRUE))+
geom_point(data=vietas_presence,aes(x=x,y=y),size=0.5,alpha=0.5)+
geom_point(data=vietas_absence,aes(x=x,y=y),size=0.5,alpha=0.5)+
coord_cartesian(ylim=c(0,1))+
scale_y_continuous(breaks=seq(0,1,0.25))+
theme_bw()+
theme(panel.grid.minor = element_blank(),
axis.title.x = element_blank())+
labs(y="Marginālo atbilžu funkcijas (cloglog)")
ggsave(attels,
filename=paste0("./SuguModeli/MarginalResponses/MargResp_",suga,".png"),
width=2000,height=augstums,units="px",dpi=120)
beigas=Sys.time()
ilgums=beigas-sakums
print(ilgums)
}Rezultātu uzskatāmībai sagatavots arī pazīmju ietekmes raksturojums 99 permutāciju procdūrā, kas attēlots kopā ar EGV VIF vērtībām.
Code
if(!require(tidyverse)) {install.packages("tidyverse"); require(tidyverse)}
if(!require(readxl)) {install.packages("readxl"); require(readxl)}
if(!require(ggtext)) {install.packages("ggtext"); require(ggtext)}
sugam=data.frame(faili=list.files("./SuguModeli/BestVarImp/"))
sugam=sugam %>%
separate(faili,into=c("sakums","suga","beigas"),remove = FALSE)
sugas=sugam$suga
for(j in seq_along(sugas)){
print(j)
sakums=Sys.time()
suga=sugas[j]
print(suga)
mainigo_tabula=read_excel(paste0("./SuguModeli/BestVarImp/BestVarImp_",suga,".xlsx"))
mainigie=mainigo_tabula %>%
filter(!is.na(final_PermImp_avg))
augstums=ceiling(length(mainigie$Nosaukums)/10)*300
pic_varimp=ggplot(mainigie,aes(x=reorder(Nosaukums,final_PermImp_avg),y=final_PermImp_avg))+
geom_col()+
geom_pointrange(data=mainigie,aes(x=reorder(Nosaukums,final_PermImp_avg),
y=final_PermImp_avg,
ymin=final_PermImp_avg-final_PermImp_sd,
ymax=final_PermImp_avg+final_PermImp_sd))+
scale_y_continuous("Pazīmes ietekme (%)",breaks=seq(0,100,10))+
scale_x_discrete(labels = function(x) stringr::str_wrap(x, width = 75))+
geom_text(data=mainigie,aes(x=reorder(Nosaukums,final_PermImp_avg),
y=103,
label=round(final_VIF,3)),hjust=0,size=3)+
coord_flip(ylim=c(0,105))+
theme_classic()+
theme(axis.title.y = element_blank(),
panel.grid.major.x = element_line(colour="grey"))
ggsave(pic_varimp,
filename=paste0("./SuguModeli/Pic_VarImp/PicVarImp_",suga,".png"),
width=1250,height=augstums,units="px",dpi=120)
beigas=Sys.time()
ilgums=beigas-sakums
print(ilgums)
}